报告题目：Geometry of Gaussian random curves

报 告 人：Andrey Dorogovtsev（Institute of Mathematics，NAS Ukraine）

报告地点：Zoom 会议ID：858 7772 7123 密码：803617

Abstract: This course aims to provide a solid introduction on the geometry of Gaussian random curves. Since the theory of geometry of Gaussian random curves is based on the concept of Gaussian random process and fields, the first part of the course will be devoted to some properties of this process and fields. And the second part of the course is devoted to discussion of geometry of Gaussian random curves like the Self-intersection local times for planar Brownian motion and the hitting probabilities for planar Broownian motion. Professor Andrey will give students some time to understand the knowledge and give some small questions about the lecture.

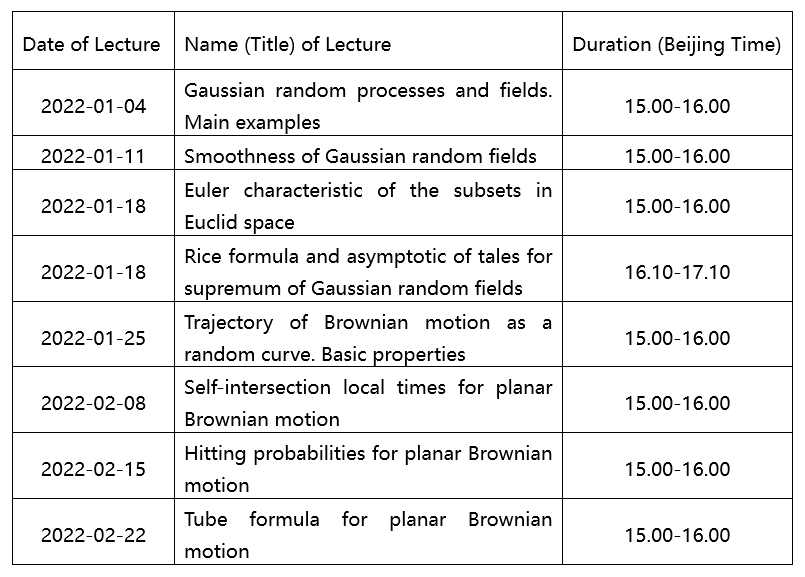
Lecture 1: Gaussian random processes and fields. Main examples

In this lecture we give the definition of Gaussian random processes and fields. Also, we will give some examples to understand this.

Lecture 2: Smoothness of Gaussian random fields

In this lecture we discuss the smoothness of Gaussian random fields, and we can get some properties on Gaussian random fields.

Lecture 3: Euler characteristic of the subsets in Euclid space

In this lecture we give the definition of Euler characteristic which in defined on Euclid space, it is topological invariant.

Lecture 4: Rice formula and asymptotic of tales for supremum of Gaussian random fields

In this lecture we give the Rice formula and discuss the asymptotic of tales for supremum of Gaussian random fields.

Lecture 5: Trajectory of Brownian motion as a random curve. Basic properties

In this lecture we discuss the trajectory of Brownian motion and give some basic properties about this.

Lecture 6: Self-intersection local times for planar Brownian motion

In this lecture we discuss the investigation of the local times of self-intersection as the most important geometric characteristics for planar Brownian motion.

Lecture 7: Hitting probabilities for planar Brownian motion

In this lecture we discuss the hitting probabilities and how we use this to describe the trajectory of planar Brownian motion.

Lecture 8: Tube formula for planar Brownian motion

In this lecture we give the Tube formula for planar Brownian motion, and use it to help us learn the trajectory of Brownian motion.

报告人简介：Andrey Dorogovtsev教授是乌克兰国家科学院通讯院士，乌克兰国家科学院数学所随机过程理论系主任，主要从事概率论及其相关领域研究，是乌克兰概率论研究方向学术领军人物之一。Andrey Dorogovtsev教授是乌克兰与德国、乌克兰与俄罗斯等国家联合项目的乌方负责人。同时，Andrey Dorogovtsev教授是《Theory of Stochastic Processes》、《Ukraine Mathematical Journal》等杂志的编委。